Multipath Delay Spread
Outline
1. 多重路徑傳播效應(Multipath Propagation Effect)
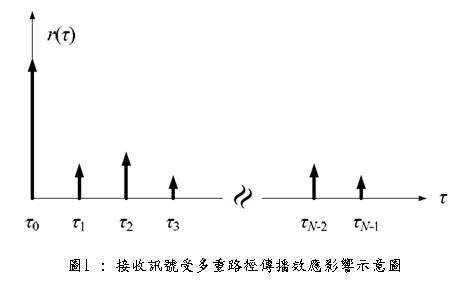
當無線電訊號由傳送端送出,經由天線送入大氣之中,此時無線電波是以發散的狀態來傳播,然後經過各個不同的路徑到達接收機。由於各個傳播路徑的環境不同,訊號將會遭受不同程度的衰減以及延遲,以圖1來表示訊號在經過多重路徑通道之後,振幅和延遲所產生的變化。
在圖1之中,利用τ
0、τ
1、...、τ
N-1 等來表示訊號經由不同路徑到達接收端時所產生的延遲,由於傳播路徑的長短不一,因此到達接收端的時間也將不同,如此便造成了多重路徑效應。因此,多重路徑效應主要是造成接收訊號在時間上的擴散效應,所以接收到的訊號時間長度,會比傳送訊號的時間長度來得大,這便是我們所謂的時散效應。圖1中不同路徑延遲的差距如果夠大,接收機便可以清楚的分辨出來,這些路徑就稱為是可解析(Resolvable)。但是,有時會有兩個甚至是多個以上路徑的訊號幾乎同時到達接收端,對接收機來說,看起來就像是同一個路徑的訊號,這些路徑就稱為是無法解析(Unresolvable)。
值得特別注意的是,在眾多無法解析的路徑之中,所謂不同路徑的訊號幾乎同時到達,這是以符元的觀點來看,先後到達的符元,由於到達時間的差異有限,所以接收機是無法分辨的;但是以載波的觀點來看,由於無線通訊系統中的載波頻率通常很高,這一點點時間上的差異,就足以造成接收訊號相位的顯著差異。這相位的差異,會使眾多無法解析的路徑,有時造成接收訊號的增益(建設性干涉),有時造成接收訊號的衰減(相消性干涉),視各路徑延遲的長短而有不同的變化。因此,對某個可解析的路徑而言,它的訊號其實是由許多不同路徑的訊號組合而成,只不過這些路徑訊號到達接收機的時間,對一個符元週期而言差距不大,所以這些路徑的符元訊號是不可解析的,而這些不可解析訊號所結合而成的接收訊號,其振幅會是一個瑞雷分布(Reyleigh Distribution)的隨機變數。
在展頻通訊系統中,如果不同路徑的延遲差距不超過一個子碼的時間,便稱這些路徑是不可解析的,反之便稱為是可以解析的。
2. 延遲擴展(Delay Spread)及功率延遲概觀(Power Delay Profile)
延遲擴展(Delay Spread)是用來描述在時域上,由多重路徑所造成的訊號波形擴散效應,簡單來說就是,由傳送端送出的一個脈衝訊號,如果通道的多重路徑效應造成數個可解析的路徑,所以在接收端會收到來自不同路徑卻包含相同資訊的訊號,每個可解析路徑的訊號皆有特定的延遲,此為著名的延遲擴展。不同的環境會有不同的延遲擴展,為了對延遲擴展做一個量化的描述,必須先介紹通道的功率延遲概觀(Power Delay Profile)。
一般在文獻上,基頻訊號的通道脈衝響應可以表示為:
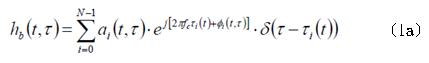
在(1a)中,符號i代表的是第i個可解析的多重路徑訊號,a
i(t,τ)代表在時間為t 、延遲為τ時的振幅,τ
i(t)則是過量延遲(Excess Delay),2πf
cτ
i(t)+Ø
i(t,τ)則是代表相位偏移,這裡所謂的過量延遲是定義成每一個路徑實際的延遲減掉第一個路徑的延遲。在此假設有N個可解析的多重路徑,故i = 0, 1, 2, ...,N−1,所以功率延遲概觀是用來描述有多個可解析路徑的通道。
通常會把相位偏移2πf
cτ
i(t)+Ø
i(t,τ)用θ
i(t,τ)來表示,θ
i(t,τ)代表的就是第i個可解析路徑訊號所有的相位偏移量。如果通道的脈衝響應是非時變性的,或是在一小段時間(距離)之內,通道的統計特性為廣義穩態(Wide Sense Stationary, WSS),則(1a)可以簡化為:
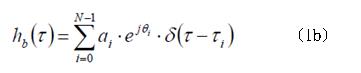
當需要量測或是預估h
b(τ)的時候,必須先傳送一個已知的訊號p(t),通常p(t)為一個脈衝訊號,可以用德塔函式(Delta Function)來表示:
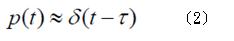
我們可以在傳送端送出p(t),如此在接收端便可得知通道的變化情形。對於小範圍的通道模型而言,通道的功率延遲概觀,便是在一個區域之內計算|h
b(t;τ)|
2對空間的平均值。因此,通道的功率延遲概觀P(τ )便可以表示為:
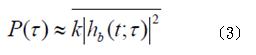
在式子(3)中,橫槓代表|h
b(t;τ)|
2 在一個區域內的平均值,而增益k 和傳送及接收訊號的功率有關。
3. 時散參數(Time Dispersion Parameters)
一般用來描述有多個可解析路徑通道的延遲特性,主要依據以下三個參數:平均過量延遲(Mean Excess Delay)、方均根(Root Mean Square, RMS)延遲擴展(RMS Delay Spread)和過量延遲擴展(Excess Delay Spread)(X dB),這些參數可以從功率延遲概觀求得,其代表意義將分別描述如下。
在有多個可解析路徑的通道中(如(1a)及(1b)所示),通常藉由平均過量延遲τ 和方均根延遲擴展στ 來量化此種通道時散的特性。平均過量延遲的定義如下:
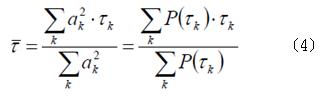
在(4)中,每個路徑的延遲τ
k皆被視為隨機變數,τ
k在經過不同權重之後所得到的平均便是τ 。而方均根延遲擴展則是定義如下:
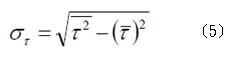
其中
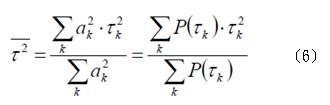
(4)以及(5)中的τ
k 是之前所定義的過量延遲,都是以第一個可偵測的接收訊號為基準來量測的,也就是說,以第一個到達接收端的訊號為準,將其延遲τ
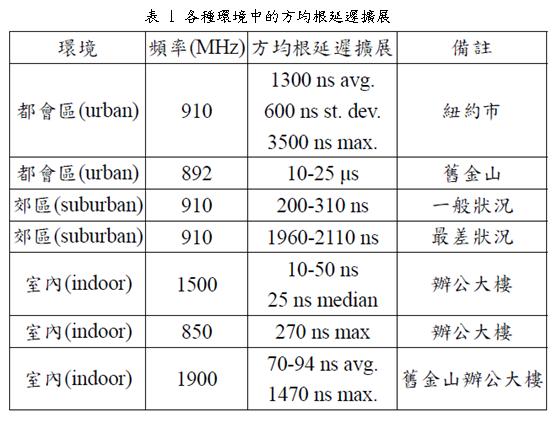
0 設定為0。值得注意的是,平均過量延遲和方均根延遲擴展是從單一個功率延遲概觀得來的,通常為了決定以上所提及參數的範圍,行動通訊業者會在許多地區做量測,以便提供給行動通訊系統使用。在戶外,方均根延遲擴展的大小通常在微秒(μ s )這個數量級;而在室內,其大小通常在奈秒( ns )這個數量級之間。表1列出了一些經由量測得來的方均根延遲擴展。
此外,功率延遲概觀的最大過量延遲(Maximum Excess Delay)( X dB)指的是,與路徑的最大能量相距X dB以內的所有路徑,找出一個延遲最大的路徑,此路徑與最大能量路徑在時間上所產生的延遲差距,就稱為最大過量延遲。換句話說,最大過量延遲就是τ
X−τ
0,其中τ
0為第一個到達接收端訊號的延遲,τ
X就是與路徑的最大能量相距XdB以內的所有路徑之中,產生最大延遲之路徑的時間延遲量。這裡要注意的是,第一個到達的訊號,其能量不一定為最大,在此只是為了方便,故假設第一個到達的訊號擁有最大能量。而τ
X有時亦稱為功率延遲概觀的過量延遲擴展(Excess Delay Spread)。功率延遲概觀的大小通常與系統所設定的雜訊門檻有關,而雜訊門檻是用來區別多重路徑訊號及熱雜訊的,如果雜訊門檻設定過低,雜訊便很容易超過此門檻而看起來像多重路徑訊號。事實上,τ 、τ
2、σ
τ也都和雜訊門檻有關,雜訊門檻設定過低的話,由雜訊引起的誤判將會使得這些參數值變高。
4. 同調頻寬(Coherence Bandwidth)
在上一小節中,介紹了一些與訊號延遲相關的參數,這些參數的值基本上是由環境所決定的,一旦用戶所處的環境是靜止不動的,這些參數的值也就不會隨著時間而改變。與延遲相關的參數,基本上是環境對訊號在時域上所產生的影響,在此將介紹一個與頻域相關的參數:同調頻寬,這個參數是由方均根延遲擴展所定義而來的。先由同調頻寬的物理意義來說明這個名詞:所有在同調頻寬B
c 範圍裡面的訊號,其所受到通道的影響是很類似的(相關性很高),也就是說,在同調頻寬內的所有訊號,有大約相等的振幅增益和線性的相位關係。若是任意兩個弦波訊號,其頻譜間隔超過同調頻寬B
c ,它們所受到通道影響的關連性就很低。
接下來要給同調頻寬正式的定義:一般定義同調頻寬的大小有兩種方式,都是以不同頻率之訊號的相關性來決定的。若是要求不同頻率之訊號的相關函式(Correlation Function)必須要大於0.9,則同調頻寬大約是:
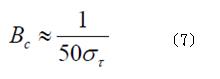
如果將同調頻寬的定義,放寬到只要求不同頻率之訊號的相關函式大於0.5,則同調頻寬大約是:
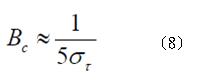
此外,也有人更進一步,把同調頻寬的定義放寬到只要求相關函式大於1/ e ≈ 0.36788。得注意的是,(7)與(8)只是一個粗略的估計,同調頻寬和方均根延遲擴展的確切關係式並不存在,而且同調頻寬的大小,也與系統的調變與解調機制有關。實際上在設計無線通訊系統時,還是必須針對特定的系統選擇正確的通道模型。
有一點特別值得注意的:方均根延遲擴展是從時域上來觀察通道的特性,同調頻寬則是從頻域上來觀察,兩者之間是成反比的關係,方均根延遲擴展越小(大)時,同調頻寬越大(小),而這兩個參數基本上都是由環境決定的,如果用戶所處的環境不變,這兩個參數基本上也不會隨著時間而改變;當然,當用戶移動或是環境隨著時間而變動時,這兩個參數也會隨著時間而改變。
5. 寬頻(Wideband)系統與窄頻(Narrowband)系統
寬頻(Wideband)和窄頻(Narrowband)是從同調頻寬衍申而來的觀念。簡單來說,所謂窄頻系統指的就是傳送訊號的頻寬小於通道的頻寬,這裡通道頻寬指的是同調頻寬。在窄頻通訊系統中,因為所有的訊號都在同調頻寬之內,所以所有的訊號都有相似的振幅增益和線性的相位響應;在窄頻系統中,系統訊號在各個頻率的增益或是衰減狀況,幾乎是一個常數,也因此稱窄頻系統的衰減是平緩衰減(Flat Fading)。值得特別注意的是,這裡的『平緩』指的是對於任意的一個固定時間,訊號在不同頻率之增益或衰減情況,幾乎是一個定值,所以平緩是一個相對於頻域的概念;然而在時域上,各個頻率訊號的增益或衰減情況,還是有可能一起經歷快速而劇烈的變化;此外,窄頻系統指的是訊號頻寬相對同調頻寬而言是較窄的,而不是同調頻寬本身是較窄的。
寬頻系統指的就是傳送訊號的頻寬大於通道的頻寬,由於訊號的頻寬已經超過同調頻寬的範圍,每一頻譜區段的訊號響應也就不盡相同,因此稱寬頻系統的衰減是頻率選擇性衰減(Frequency Selective Fading);很明顯的,這也是一個頻域上的概念,而隨著時間的改變,各個頻率的增益或衰減情況,還是有可能經歷不同的消長;同樣值得注意的是,寬頻系統指的是訊號頻寬相對同調頻寬而言是較寬的,而不是同調頻寬本身是較寬的。寬頻系統和窄頻系統的差別,可以藉由圖2來了解。
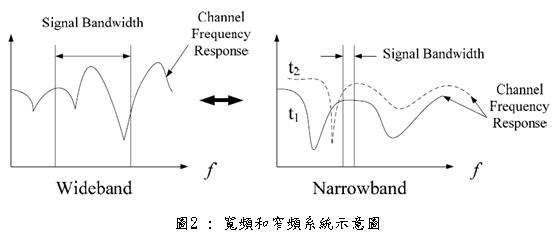
綜合以上所說的,先由通道的時散性定義出方均根延遲擴展,再由方均根延遲擴展定義出同調頻寬;把訊號頻寬和同調頻寬比較,訊號頻寬較窄的,稱為窄頻系統,訊號頻寬較寬的,稱為寬頻系統;窄頻系統會遭受平緩衰減,寬頻系統會遭受頻率選擇性衰減。以下便對多重路徑效應所產生的衰減做一個整理。
一、 平緩衰減(Flat Fading);窄頻(Narrowband)系統
1. 訊號頻寬<通道頻寬(同調頻寬)
2. 延遲擴展<符元週期
在一個平緩衰減的通道中,當訊號頻譜經過通道之後,因為各個頻率的衰減
狀況是類似的,頻譜仍然可以保有它原本的特性而不會變形。然而因為多重路徑的效應,通道的衰減狀況有可能隨著時間而變,接收到的訊號強度也會隨著時間而改變,整個平緩衰減通道的特性是如圖3所示。
在圖3之中,傳送訊號s(t)的符元週期大於通道的延遲擴展,也就是說訊號的頻寬是落在通道的同調頻寬之內,接收訊號r(t)在時間上雖然會受到通道增益變化的影響,所以訊號的振幅會隨著時間而改變,但是訊號頻譜R( f )的形狀並不會有太大的變化,頂多是因為通道的增益隨著時間改變,而導致訊號頻譜整個放大或縮小。然而,當通道產生嚴重衰減(Deep Fade)時,訊號的各個頻率分量都會遭受嚴重的衰減,此時只有透過增加傳輸功率,才可能保持原有的通訊品質,而所需要增加的功率,有可能到達原先的20至30dB。這裡的平緩衰減,也有人稱為頻率平緩衰減(Frequency-Flat Fading)。
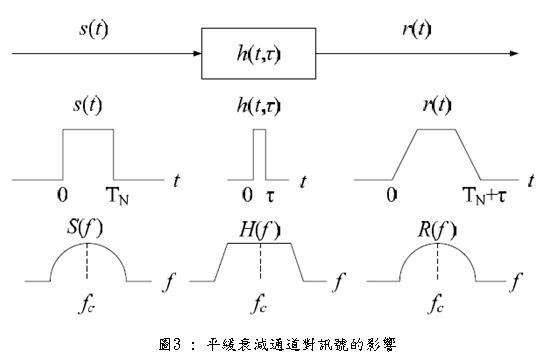
此外,在平緩衰減通道中,由於通道的延遲擴展小於符元的週期,所以所有的多重路徑訊號,雖然到達接收機的時間先後不一,但是對接收機而言,這些訊號是不能解析的,也就是所有多重路徑訊號結合的結果,會形成單一個可解析的路徑,這個路徑訊號的振幅是一個隨機變數,而一般認為這是一個瑞雷分布(Rayleigh Distribution)的隨機變數。
二、 頻率選擇性衰減(Frequency Selective Fading);寬頻(Wideband)系統
1. 訊號頻寬>通道頻寬(同調頻寬)
2. 延遲擴展>符元週期
相較於以上所提的窄頻系統,如果通道維持固定振幅增益和線性相位響應的頻寬,小於傳送訊號的頻寬時,便稱此通道為頻率選擇性衰減通道。在此情況下,因為通道的延遲擴展大於符元的週期,因此多重路徑的綜合效應,會在接收端形成數個可解析的路徑,當然,每一個可解析的路徑還是包含了數個不可解析的路徑。因此,傳送端所發射的同一個訊號,將會在接收端收到數個不同延遲的訊號,同一個訊號在不同的時間到達,彼此之間就會造成干擾,因此訊號將會有失真的情形發生,這種干擾是另一種形式的符際干擾。這裡所謂的符際干擾和一般數位通訊系統的符際干擾是不一樣的,一般數位通訊系統的符際干擾指的是鄰近符元間所產生的干擾,而頻率選擇性衰減通道所產生的符際干擾,則是來自同一個符元。
從頻域的觀點來看,通道的頻率選擇性衰減會使不同頻段的訊號,遭受到不同大小的增益與衰減,這也是為什麼稱這種通道為頻率選擇性衰減的原因。從時域的觀點來看,同一個傳送訊號會在不同的時間到達,這就是頻率選擇性衰減通道的時散效應。圖4介紹了頻率選擇性衰減通道的特性,可以看出訊號的頻寬是比通道的同調頻寬來的大,而且通道在不同的頻段有不同的增益。從時域的觀點來看,因為各個頻率的衰減或增益程度會隨著時間而有不同的變化,所以接收訊號r(t)的失真情況也會隨著時間而改變。
在頻率選擇性衰減通道之中,各個可解析路徑的訊號之間,雖然會有符際干擾而使訊號失真,然而各個路徑的衰減狀況是相互獨立的,這也是另一種形式的多樣性(Diversity),對接收訊號提供了額外的保護,如果有某幾個路經遭受嚴重的衰減,接收機可以藉由其他的路徑來還原傳送的訊號。從頻域的觀點來看,因為不同頻段所遭受到的衰減狀況不同,如果有某幾個頻率遭受嚴重的訊號衰減,接收機可以從其他的頻段來還原傳送的訊號。
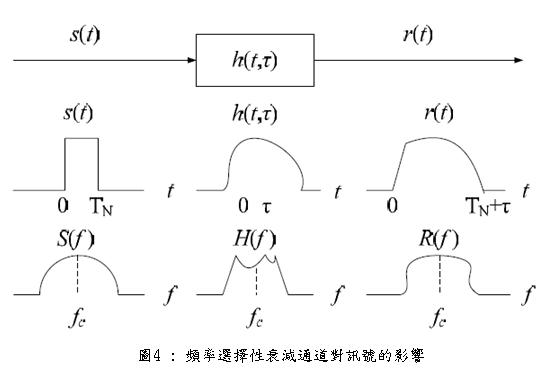
對頻率選擇性衰減通道來說,因為多重路徑的綜合效應會在接收端形成數個可解析的路徑,因此在使用電腦模擬頻率選擇性衰減通道時,會把幾個相互獨立的平緩衰減通道結合在一起,並把訊號經過每一個平緩衰減通道之後的振幅當成是一個隨機變數,而這些隨機變數都是相互獨立的瑞雷分布,每一個平緩衰減通道有各自的訊號平均功率,各通道之間也都在時間上有不同的延遲把它們區隔開來。
經由以上對平緩衰減和頻率選擇性衰減的解釋,可以在時域上依延遲擴展的程度、或是在頻域上依通道頻寬的大小來區分上述兩種衰減,整個平緩衰減和頻率選擇性衰減的關係是如圖5所示。
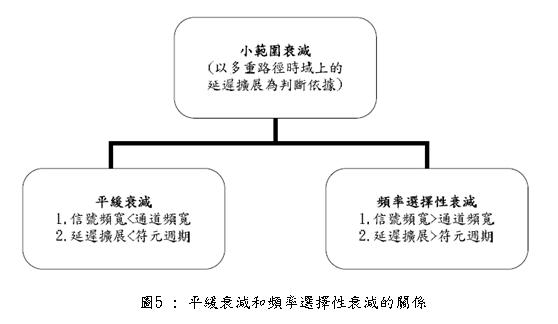
值得特別一提的是,無線通訊系統本身並沒有絕對屬於寬頻系統或是窄頻系統,無線通訊系統屬於寬頻或是窄頻都是要由系統當時所處的環境來決定。同一個系統,有可能當它在室內的環境時,因為方均根延遲擴展較小、同調頻寬較大,而屬於窄頻系統;當這個系統拿到戶外的環境時,有可能因為方均根延遲擴展較大、同調頻寬較小,轉而屬於寬頻系統。
Reference
Wikipedia
http://en.wikipedia.org/wiki/Delay_spread/
楊慶隆 "MCCDMA A technique : OFDM+CDMA" 國立東華大學
http://sna.csie.ndhu.edu.tw/~cnyang/MCCDMA/sld037.htm
Wireless Communication
http://www.wirelesscommunication.nl/reference/chaptr03/fading/delayspr.htm